How To Solve a Magic Square

---

Let's look at a 4 x 4 magic square.

Basic Rules to solve the magic Square:

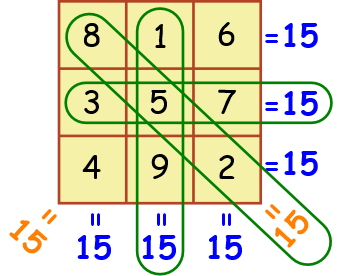
Fill in the small squares inside the large square with the consecutive integers from 1 to 16 so that the sum of all rows, columns, and diagonal are the same number - which is the "Magic Number".

• Determine the Magic Sum of your 4 x 4 magic square.

Below is the an "Algebra" formula that we can use to help determine what our "Magic Sum" can be. Since we're working with a 4 x4 magic square, the Order of our magic square is 4. See formula below: 

• Place the number 1 in the center box on the top row.

This same thing is done for any magic square with an odd number of columns or rows. 

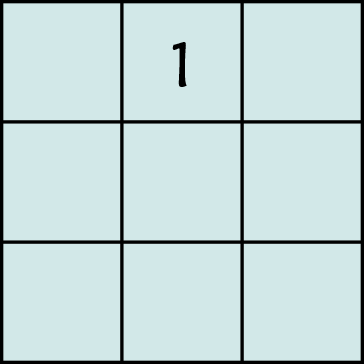
• Follow an up-one, right-one pattern to fill in the remaining numbers.

Start at the middle box in the top row where you placed the 1. Move up one row and to the right one column and write in the next number sequentially. Whenever a move takes you above the top row (like the first move will), go to the bottom row instead. If you need to move a square to the right but are already in the rightmost column, move to the leftmost column instead. Continue filling in the square following the pattern until it’s complete.

5. **Numerical Patterns:** Magic squares contain intriguing numerical patterns that captivate mathematicians and enthusiasts alike.

6. **Cultural Diversity:** Different cultures have developed their own variations of magic squares, each with its unique properties and rules.

7. **Mystery and Challenge:** The challenge of constructing and solving magic squares adds an element of mystery, making them a lifelong pursuit for math aficionados.

8. **Educational Value:** Working with magic squares can enhance mathematical skills, including addition, problem-solving, and pattern recognition.

9. **Mind-Bending:** The concept of magic squares is mind-bending, as the mathematical rules governing them are not immediately obvious.

10. **Versatile Application:** Magic squares find applications in various fields, from recreational math to art, cryptography, and even some areas of science.

11. **Cognitive Benefits:** Solving magic squares can improve cognitive functions such as memory, attention, and logical reasoning.

In summary, magic squares are a captivating fusion of mathematics, history, art, and culture, making them an endlessly fascinating topic for exploration and enjoyment.

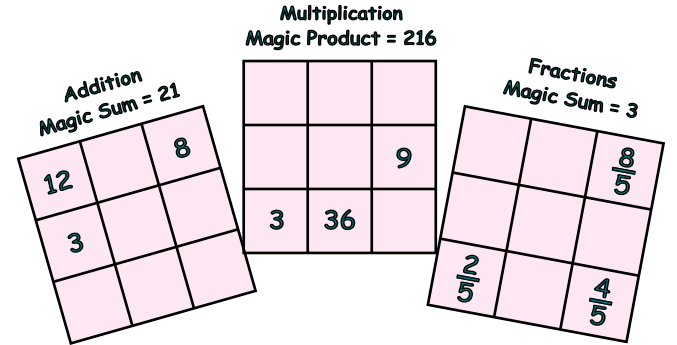
1.

Let's say we are trying to solve a 4 x 4 magic square...

The Magic Sum for the magic Square  is 34. This means all the rows, columns, and diagonals of the magic square have to add up to 34 using the consecutive integers: 1 through 16.