Teaching Times Tables

A hands-on way to learn times tables

Yes, some kids have trouble memorizing..., so having more than one way of teaching times tables can be a life-saver teachers and parents since some kids really struggle memorizing their tables!

There are some pretty creative ways to help kids get around the traditional rote memory method to learn their times tables and here's one that might click with your kid/s.

Or this could be a good way to help students with those certain times tables that really have a hard time remembering. Sometimes, it's just certain ones they really have a hard time remembering.

Here's How It Works:

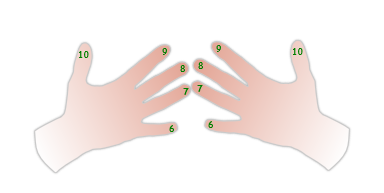
As you see in the picture, each finger on the hand is given a specific number, 6 through 10. The fingers on both hands are numbered the exact same way.

Pinkie - 6

Ring Finger - 7

Middle Finger - 8

Index finger - 9

Thumb - 10


Let's walk through an example to explain how it works:


Example 1:

7 x 7

The first step is touch the two fingers of the numbers you're multiplying together as you can see in the picture below. See how the two ring fingers, which are designated 7, are touching....

teaching times tables for kids 7 x 7

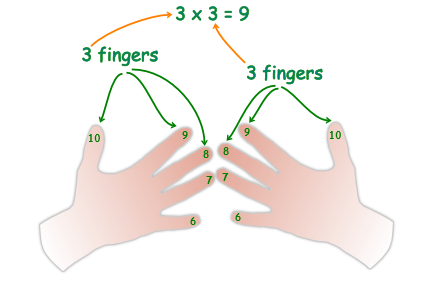
The second step is to count the number of fingers on each hand, above the two fingers that are touching, and then multiply these two numbers together.

For our example, there are the three fingers above the two fingers touching on the left hand, and there are also three fingers above the two fingers touching on the right hand. So we multiply: 3 x 3 and get 9. Check out picture below....

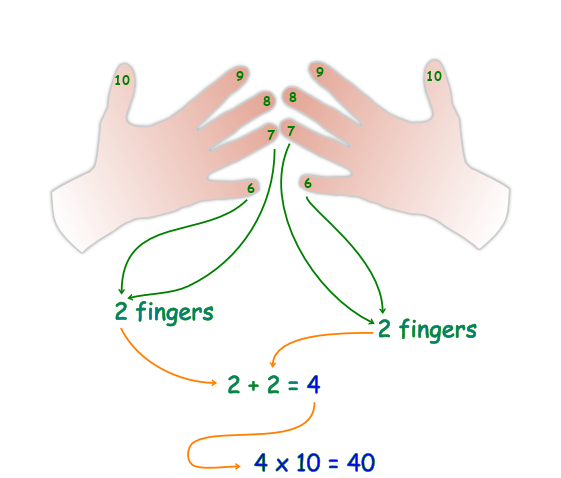
teaching times tables step 2 example 1

The third step is to count the number of fingers below two fingers touching as well as the two fingers touching and multiply this total by ten.

For this example, there are four fingers total, so we multiply: 4 x 10 and get 40.

The last step is to add these two numbers from the previous two steps:

40 + 9 = 49 

And so we get:

 7 x 7 = 49 

Return from How Teaching Times Tables Learn With Math Games Home

Go to main Mutilplication Games page

Please note that all fields followed by an asterisk must be filled in.

Please enter the word that you see below.

  

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.