- Home
- Multiplication Games
- Napiers Bones
Napiers Bones
A Fun and Easy Way To Multiply Big Numbers
Napiers bones is a method that makes multiplying large numbers easy! This multiplication method was used for more than 300 years until the invention of mechanical calculators. The reason they were called Napier’s Bone’s, was because they were made out of bones.
Multiplying large numbers may be a bit tricky for students. But after learning Napier's method, they'll see how fun and cool it can be! Students actually enjoy multiplying large numbers using the Napier's Bones Method!
A fun, cool, hands-on method for students to enjoy multiplying large numbers in a different way.
The great thing about multiplying using Napier's method, is you only need to know your times tables from 1 to 9! And the rest is just addition!
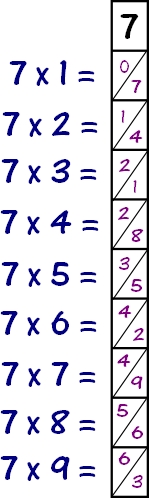
Make Your Own Napiers Bones
It's a quick and easy process that even younger students can do.
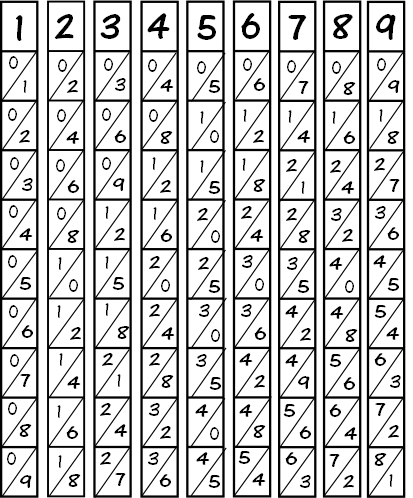
- Print Napier's Multiplication Grid
- Use scissors to cut along the vertical lines so that you have separate columns. (See picture on right.)
These are your Napier's Bones. Just in case you're wondering, they're also referred to as Napier's Rods.
- Optional: For best results, you may want to have them laminated to make them last longer for continued use.
You may want a blank set of Napier's bones that your students can fill out to get practice with their multiplication tables for 1 to nine.
Now let's try an example multiplication problem.
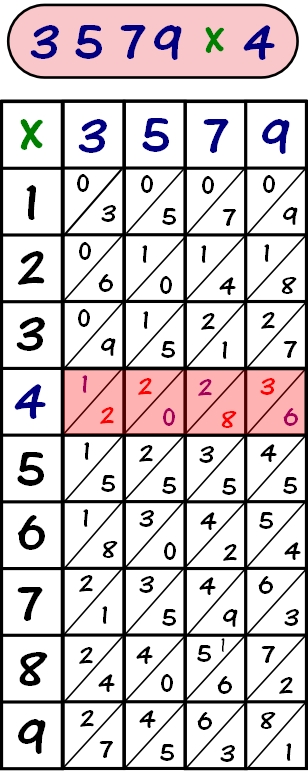
Let's say we want to Multiply:
3579 x 4
- Lay out the bones that have the top numbers 3, 5, 7, and 9. (See picture on right.)
- Starting from the right side, in the 4th row, add the two numbers in each diagonal of that row, and then write its sum underneath that column. (See picture on right.) You can see the 4th row highlighted in picture.
- If you get a two-digit sum, you will need to write down the ones digit, and then carry the other digit over to the next diagonal to the left to be added with it. See picture.
So in the picture below, I'm just showing you the 4th row. Notice the the diagonal with the 8 and the 3. Since 8 + 3 = 11, we wrote the 1 underneath, and carried the other 1 to the diagonal to its left.
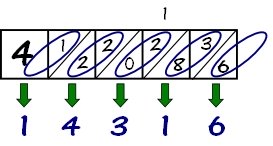
~ And that's the answer! ~
14,316
Pretty Cool. huh
Ready for another one! Let's take the same 4 digit number and multiply by a 2 digit number ending in zero.
Now Let's Multiply
3579 x 80
- Lay out your bones the same way as the example above so that the top numbers for the bones are 3, 5,7, and 9.
- Multiply 3579, by the number furthest to the left of the other number, in this case 8, following the same steps above. Note that 8 is in the Tens place.
- Since 8 is in the Tens place, we just add one zero to the end of the product and the result is 3579 x 80. And that's our answer! See picture below.
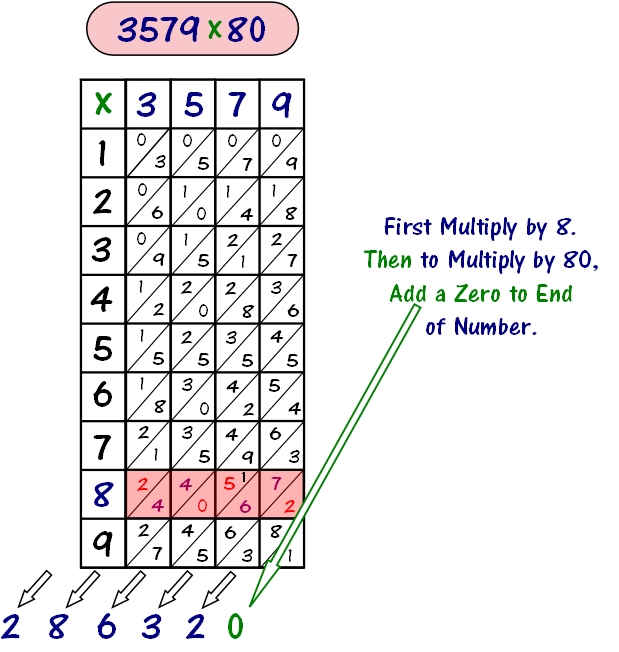
~ And that's the answer! ~
286,320
Now that you know how use Napier's Bones to multiply by a 2-digit number ending in zero, I'm going to show how to multiply a 4-digit number by a 2-digit number that does not end in Zero. See picture below.
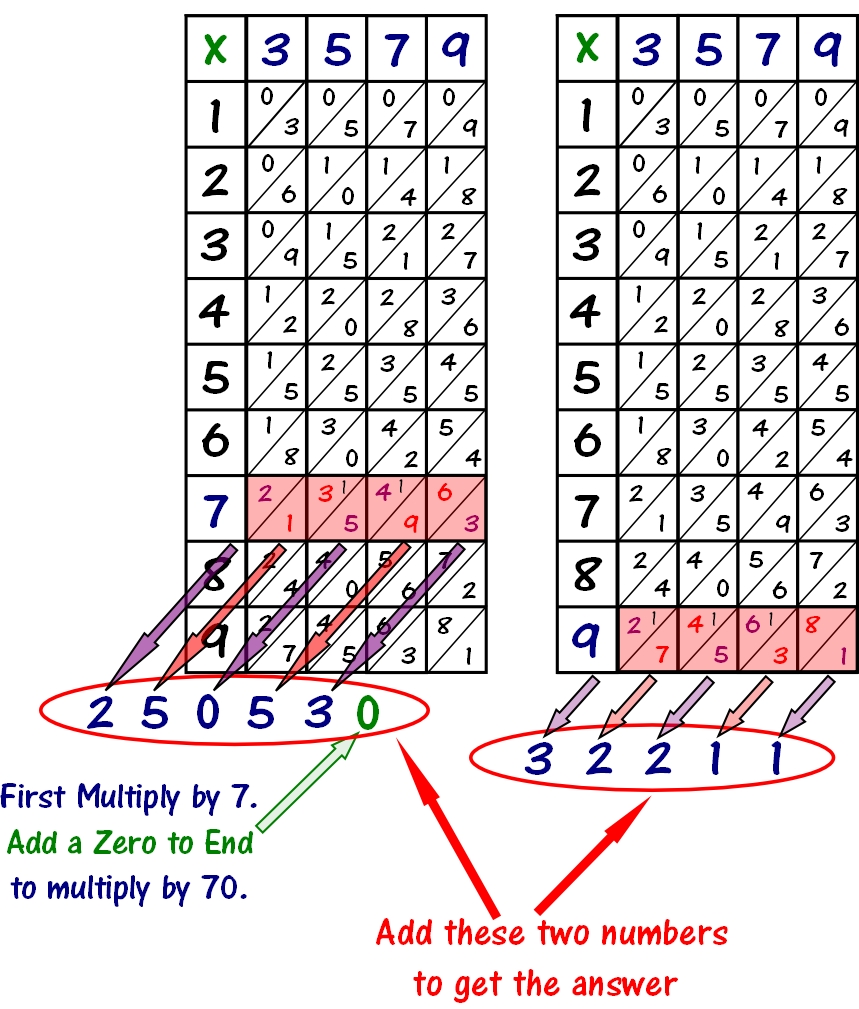
Now let's Multiply
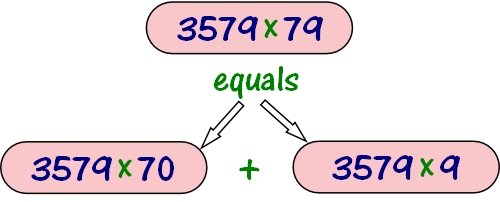
3579 x 79
- To multiply 3579 by a number that doesn't end in zero, first multiply 3579 by the number to the left of the zero using Napier's method as explained above. (3579 x 7)
- If the the number you're multiplying by is in the Tens place, as in this example, add one zero to the result. (if you are multiplying a by a number in the Hundreds place, add two zeros, and so on...)
- Next, use Napier's method to multiply 3579 by the Ones digit of 79. (3579 x 9)
- Finally, add this value to the value you got above to get the final answer. See picture below.

Here's a short video explaining
And there you have it! I'm going to put up some worksheets on this page in the next couple of days with multiplication problems that students can try using the Napier's Bones method. Let us know if you have any questions.
Go to Multiplication Games page
Return to Learn With Math Games Home
Fun-Multiplication
New Way to Multiply by Drawing Squares!
Multiplying Fractions with Rectangles:
Fraction Multiplication is easy just by Drawing Rectangles.
Multiplying Memorization Made Easy:
Memorizing Multiplication Tables has never been so easy!