Algebra Tiles

"Hands-On Algebra"

If you like the hands-on approach to teaching, then maybe you know about algebra tiles. Check out the video below to learn more about how they can help engage your algebra students.

The tiles are good manipulatives to give students a hands-on approach to be used in addition to the normal way it's taught in the classroom.

Let's see how we can use "algebraic tiles to model operations involving integers".

Adding Integers with Tiles

algebra tiles

The yellow square represents a +1 (positive 1).

The red square will represent a -1 (negative 1).

  • When you put these two squares together, their sum is zero.
  • A yellow and red square together can be referred to as because as we said above when added their sum is zero.

Let's try this example....

(+4) + (-2)

Step 1: Lay out the appropriate tiles for your addition problem. In our example of (+4) + (-2), we need to lay out four yellow squares and two red squares.

adding integers - algebra tiles

Step 2: Circle the zero pairs. So below you can see we have circle two zero pairs.

algebra tiles - zero pairs

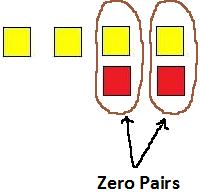
Step 3: Remove the zero pairs, and whatever squares you have left will be the answer to the addition problem. You will always have just one color left, either red or yellow. So in this case we have two yellow squares left.

algebra tiles - adding integers result

So the answer to the problem is......

(+4) + (-2) = (+2)

Solving One Step Algebra Equations with Tiles

One of the first things algebra students learn, and most seem to remember is "whatever you do to one side of the equation, you have to do to the side of the equation too!"

For our first equation, let's solve:

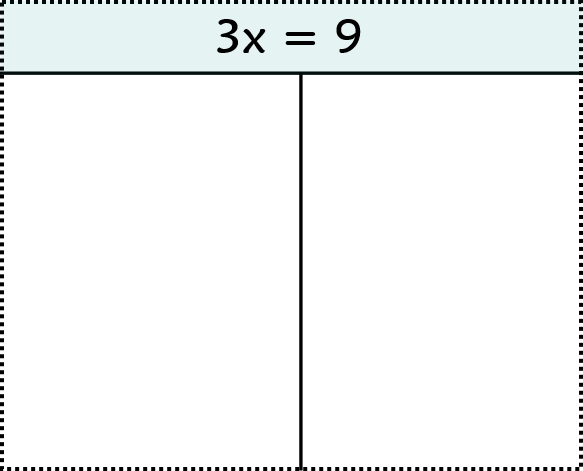
3x = 9

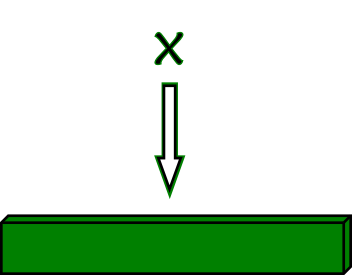
First, we need to introduce the variable x, and in our algebra tiles, it's represented by a long green rectangle as seen below:

x bar

Steps To Solve Equation:

  • Write the equation at the top of the paper and draw a vertical line from the equal sign down the paper. The vertical line drawn separates our equation into a "left-side" and a "right-side".
algebra one-step equation

The "Goal" of solving any algebra equation is

to get the variable by itself on one side of the equation.

Our variable here is "x".

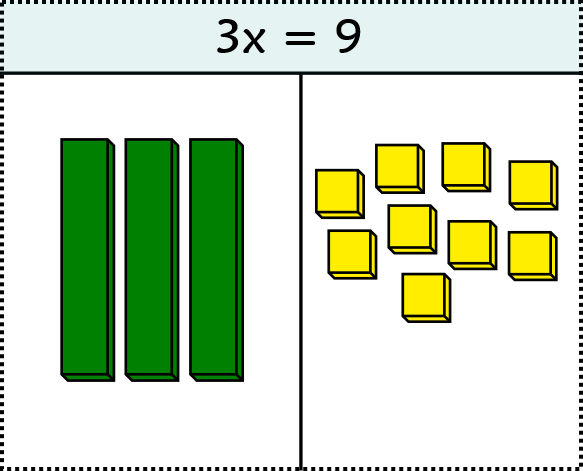
  • Use the algebra tiles to "model" the equation on each side:
model algebra equation
  • Next, take the side with the x tiles and divide it into equal groups of x, so therefore we divide into three groups of one x each. See picture below:
three groups of x tiles

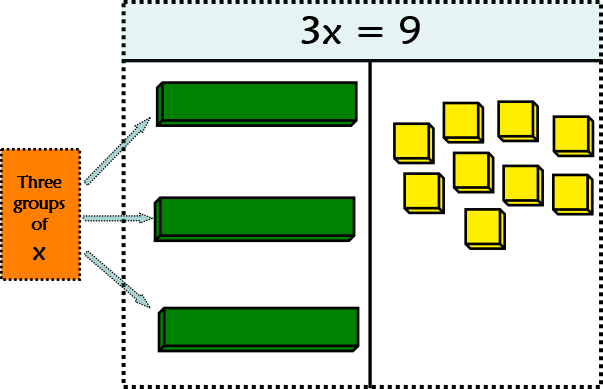
We know in algebra, whatever we do to "one side of the equation", we have to do to the "other side of the equation".

  • So therefore the next step is to divide the yellow tiles into three equal groups.
three equal groups of unit tiles

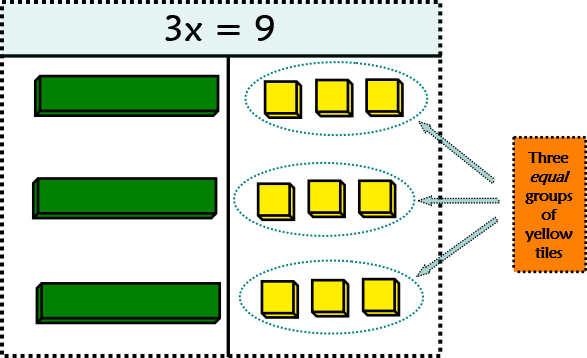
So now we see that

x = 3

So we Solved the Equation!

Solving Multistep Algebra Equations with Tiles

You might want to check out this video explaining how the tiles work.

There are a variety of hands-on approaches to teaching algebra in the classroom or at home if you home school. Besides the regular text book methods most of us grew up on, many more teachers and schools are integrating hands-on teaching methods and finding them to be very effective.

Studies have shown that when kids are more interested in the subject matter, they tend to learn material better and their retention rate also improves. Besides, if they are enjoying them selves more it makes your job that much more enjoyable.

Go to main Algebra Games page

Return from Algebra Tiles page to Math Games Home

Please note that all fields followed by an asterisk must be filled in.

Please enter the word that you see below.

  

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.